Image Filtering: Transforming and Enhancing

Image Filtering: The Artist’s Toolkit

If image representation is the canvas and pixels are the paints, then image filtering is the artist’s brush, capable of creating a myriad of visual effects and enhancements. Image filtering involves applying specific mathematical operations to modify the pixels within an image, altering its appearance or extracting valuable information.

Convolution: The Heart of Filtering

Convolution is the fundamental operation underlying many image filters. Imagine a small matrix (called a kernel or filter) sliding over the image, pixel by pixel. At each position, the kernel multiplies its values with the corresponding pixel values in the image, and the results are summed up to produce a new pixel value. This process effectively blends the pixel’s neighborhood, leading to different filtering effects depending on the kernel’s values.

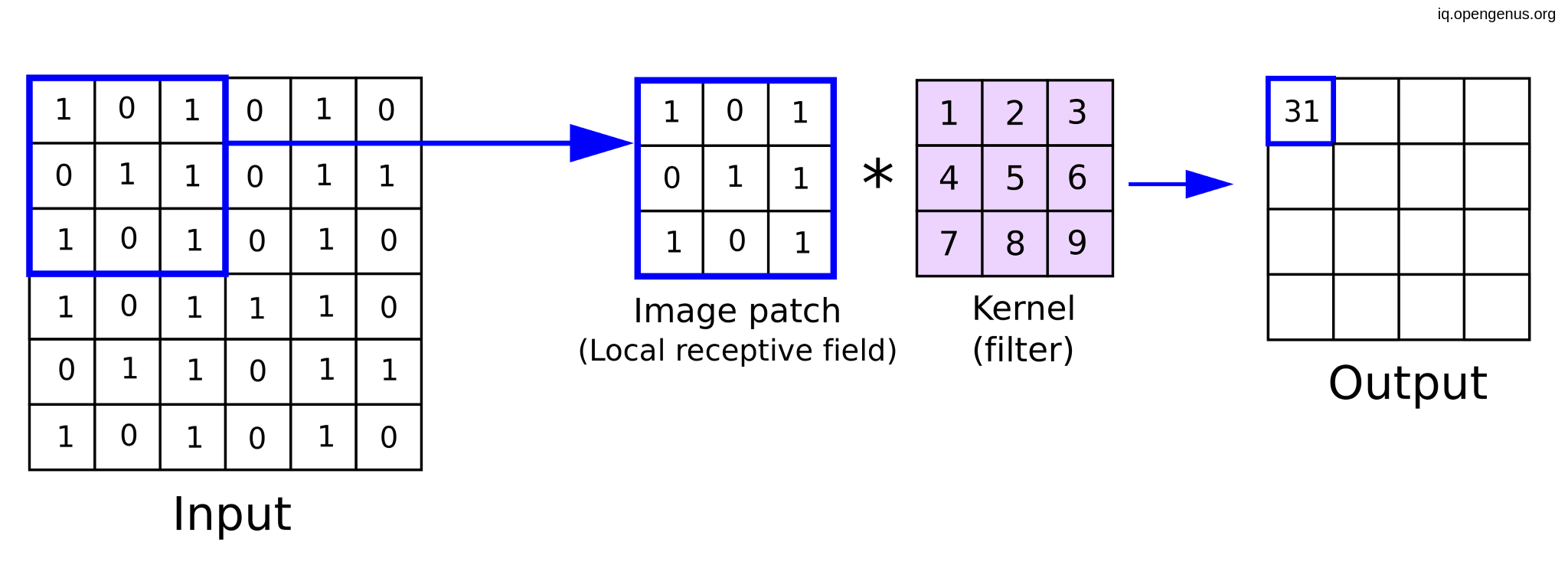
Linear Filters: Weighted Averages

Linear filters are a straightforward class of filters where the output pixel values are a weighted sum of the input pixel values. Some classic linear filters include:

• Blurring (Low-Pass) Filters: These filters smooth out an image by averaging pixel values within a local neighborhood. They reduce noise and fine details.
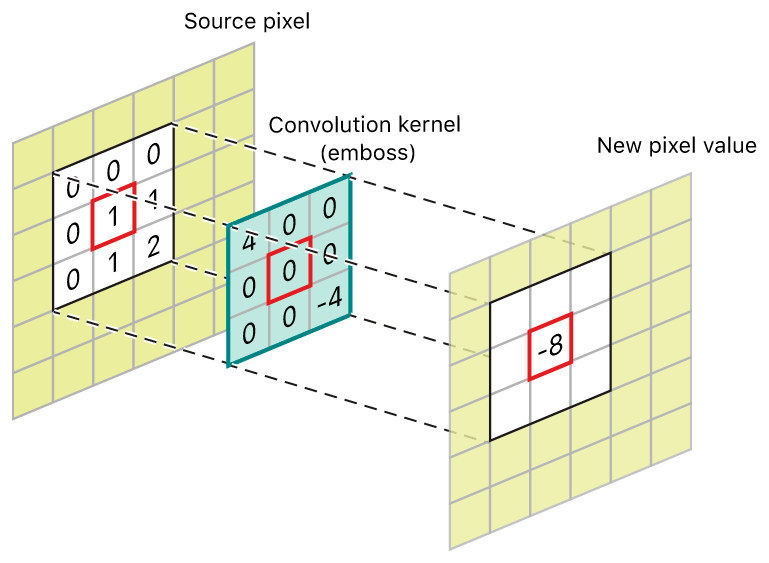
  • Example: A Gaussian blur uses a bell-shaped Gaussian distribution to weight the pixels, creating a natural-looking blur.
• Edge Detection (High-Pass) Filters: These filters emphasize edges and boundaries within an image by highlighting areas of rapid intensity change.
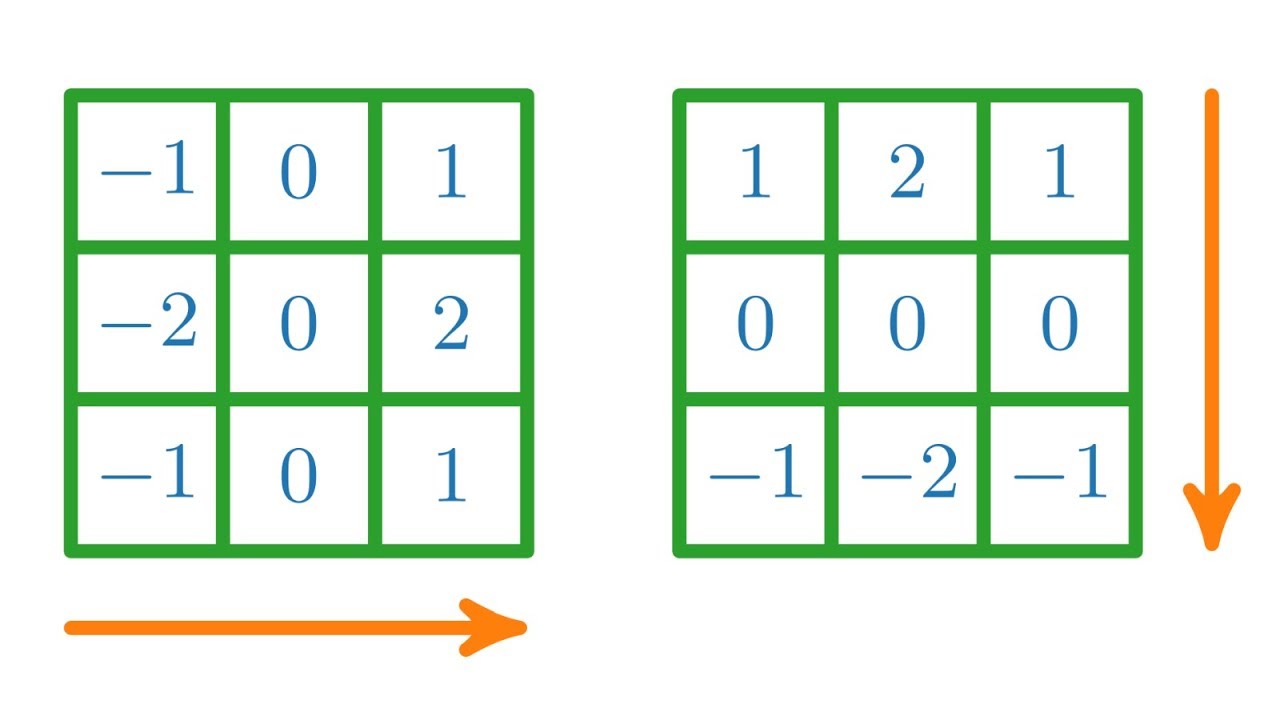
  • Example: A Sobel filter is a common edge detector that calculates gradients in the x and y directions to identify edges.

Non-Linear Filters: Beyond Weighted Sums

Non-linear filters don’t follow the simple weighted sum rule of linear filters. They often use more complex operations to achieve specific effects.

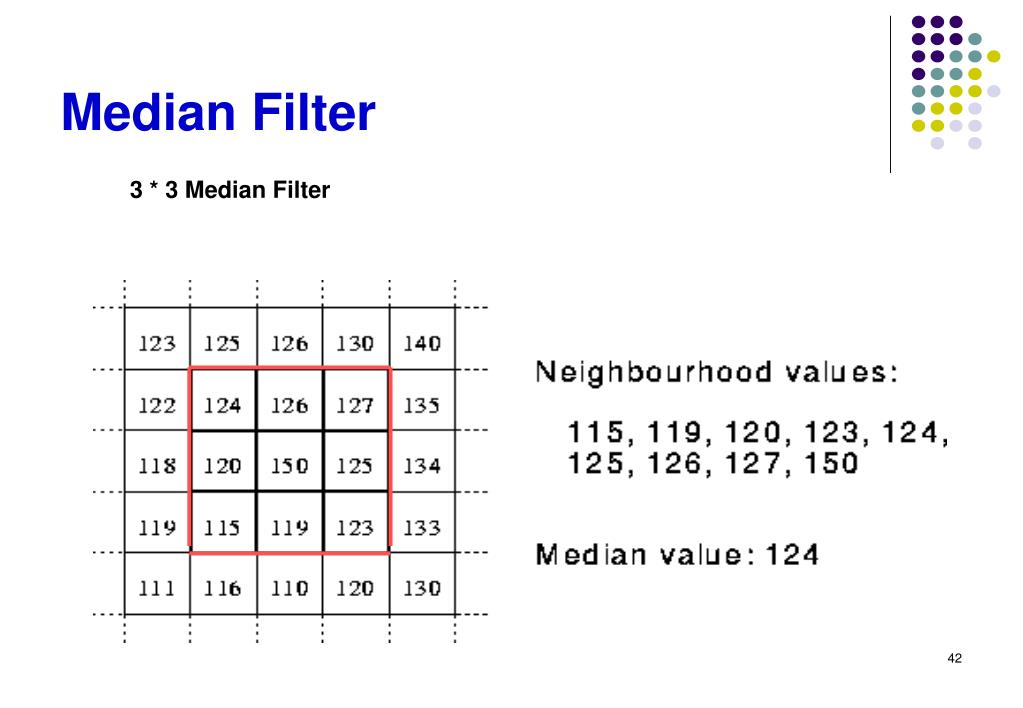
• Median Filter: Excellent for noise removal, the median filter replaces each pixel with the median value of its surrounding pixels. It’s particularly effective at removing salt-and-pepper noise while preserving sharp edges.

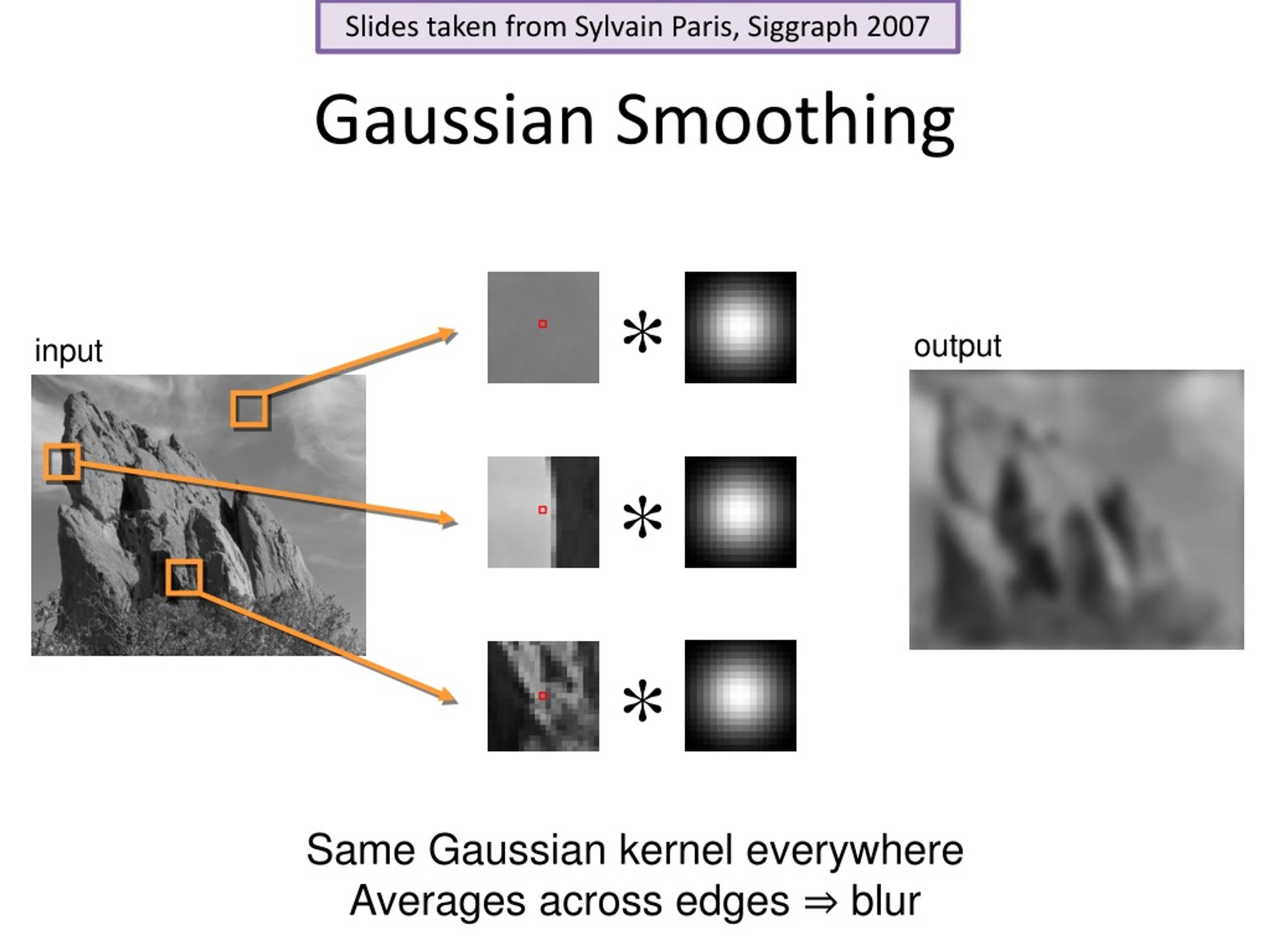
Gaussian Smoothing: A Gentle Touch

Gaussian smoothing, also known as Gaussian blur, is a popular blurring filter. It uses a Gaussian function to assign weights to pixels based on their distance from the center. The result is a soft, natural-looking blur that effectively reduces noise and fine details.

Sharpening: Bringing Out the Details

Sharpening filters do the opposite of blurring – they enhance edges and fine details, making images appear crisper. One common approach is to subtract a blurred version of the image from the original image, effectively amplifying the high-frequency details.

Formula for Sharpening:

Sharpened Image = Original Image + (Original Image - Blurred Image) * Amount

The “Amount” parameter controls the degree of sharpening.

Let’s Get Practical!

Many software tools and libraries (like OpenCV) make it easy to apply these filters without having to implement the formulas yourself. You can experiment with different kernels and parameters to create a wide range of artistic and practical effects.

Applications of Image Filtering

Image filtering plays a pivotal role in various fields:

• Image Enhancement: Improve image quality, reduce noise, and correct color imbalances.
• Feature Extraction: Identify key features like edges, corners, or textures for object recognition and tracking.
• Medical Imaging: Enhance medical scans to aid in diagnosis and treatment planning.
• Artistic Effects: Create visually appealing styles and filters for photographs and videos.

Delving Deeper

This is just a glimpse into the vast world of image filtering. There are countless other filters and techniques to explore, each with unique properties and applications. Understanding the principles of convolution and the different types of filters opens up a whole new realm of possibilities for image manipulation and analysis.

Feel free to ask if you have any more questions or want to explore specific filtering techniques in more detail!